Theoretical proficiency in billiards (ONLY)

Fares Al Rwaihy

May 21, 2023

Explore the high-velocity effects and short-duration contacts that make billiards dynamic and exciting.

8 min read

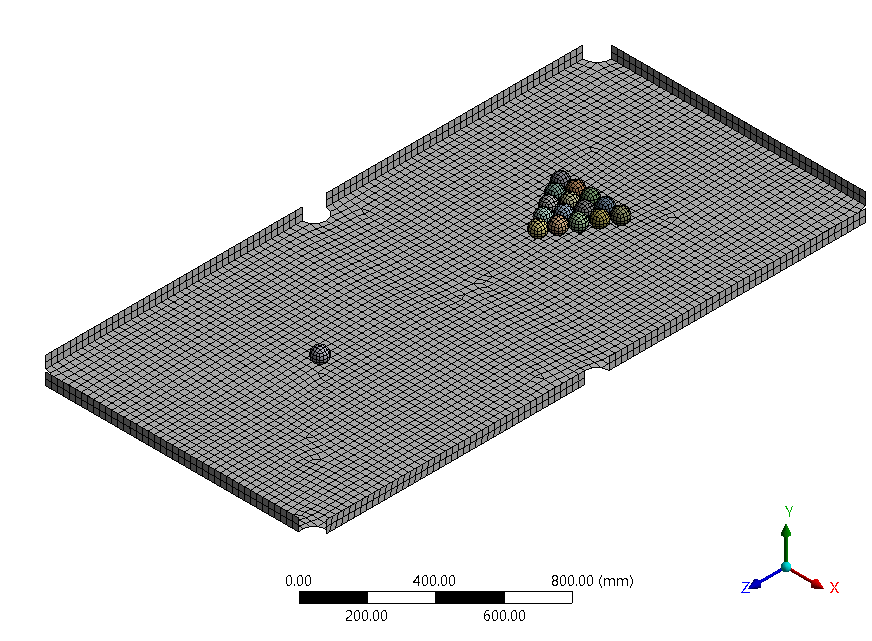
Billiard in FEA simulation

It's funny that I can analyze a billiard game using FEA, even though I struggle to score a goal in real life. Nevertheless, let's start our analysis with a lighthearted video where everyone is joyous over my successful goal.

Overview

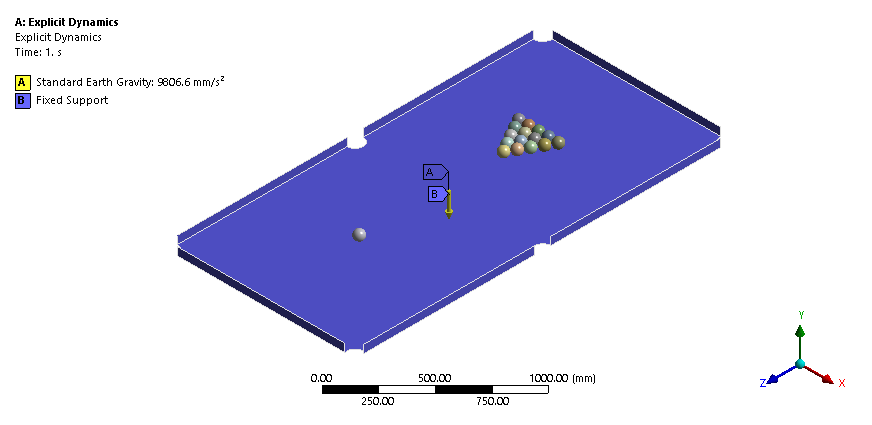
This simulation uses a Billiard Ball Collision to illustrate how Explicit dynamics analysis can be used for short duration contact problems. Explicit dynamics is chosen because the dynamic effect cannot be ignored, and the time step needs to be small to capture the high velocity and short duration contact.

**Thanks to Ansys innovation courses for enhancing this blog with an idea

Mesh

Two different meshing techniques were employed in the Finite Element Analysis (FEA) of the billiard game. A fine mesh was utilized for the billiard balls due to their high variability and complex behavior, requiring more elements to accurately represent their characteristics. On the other hand, a coarser mesh was used for the billiard table, considering its significantly larger size compared to the balls. This approach was chosen to optimize computational efficiency and reduce the solving time for the FEA simulation while still capturing the essential features of the table's behavior.

Boundary Conditions

To streamline the analysis process and optimize computational efficiency, friction was not taken into account in this study. This decision was based on the assumption that the sweet spot (hitting spot) on the billiard ball minimizes friction since there is neither slipping nor a high coefficient of friction at that specific location. Additionally, for the sake of simplification, the billiard balls were considered as rigid bodies rather than accounting for their small deformation changes. This approximation significantly reduces computational time and allows for a more efficient analysis of the billiard game.

Results

Each set of velocity values has a direct impact on the position and motion of the balls. Through Repeating and error, I discovered that by utilizing specific numbers, I achieved a powerful break speed of 11 m/s in the minus Z direction, accompanied by a lateral speed of 0.035 m/s in the X direction. This combination of velocities allowed me to successfully score a goal.

Summary

This simulation uses explicit dynamics to simulate the process of billiard balls collision. Explicit dynamics is suitable for this type of simulation because it involves high dynamic effects and short duration contact. All the parts are set to rigid bodies to save computational time. The relationship between time step and contact is also illustrated in this simulation: the time step needs to be small enough to capture the short contact duration, otherwise unrealistic contact penetration will happen.

Energy Conservation in Billiards

Energy conservation is a key concept in billiards, ensuring that the total energy of a system remains constant before and after ball collisions.

E_{in}\:=\:E_{out}

During ball collisions in billiards, energy is transferred between the balls involved. Kinetic energy is the energy possessed by an object due to its motion, while potential energy is the energy stored in an object based on its position or configuration.

KE_{in}+PE_{in}\:=\:KE_{out}+PE_{out}

However, it's important to note that in an idealized scenario with perfectly elastic collisions, the total kinetic energy before and after the collision remains constant.

\frac{1}{2}m_A\left(V_{A,in}\right)^2\:=\:\:\frac{1}{2}m_A\left(V_{A,out}\right)^2+\frac{1}{2}m_B\left(V_{B,out}\right)^2

Assuming the masses of billiard balls are equal with elastic collision, we can simplify the conversation of kinetic energy

\left(V_{A,in}\right)^2\:=\:\:\left(V_{A,out}\right)^2\cdot \:\left(V_{B,out}\right)^2

This is due to the conservation of mechanical energy. In practical situations, some energy may be lost to various factors such as friction, rotational motion, deformation of the balls, sound, and heat.

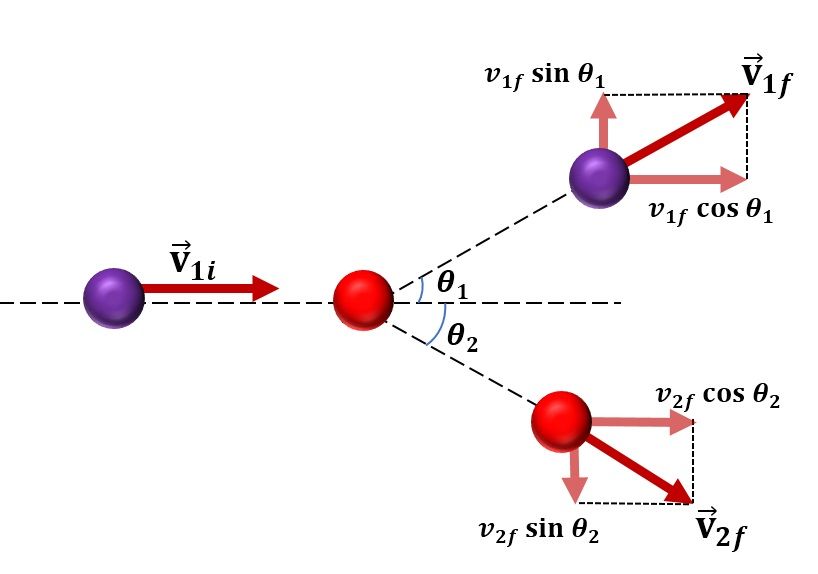
Momentum Equations

Momentum is a fundamental concept in physics that plays a significant role in billiards. It describes the quantity of motion possessed by an object and is determined by its mass and velocity. Understanding momentum is crucial in predicting ball trajectories and planning shots in billiards.

When a billiard ball strikes another ball, momentum is transferred from the striking ball to the target ball. The amount of momentum transferred depends on factors such as the mass and velocity of the balls.

P_{in}\:=\:P_{out}

As a result of the collision, the striking ball loses some of its momentum, while the target ball gains momentum. This means that the combined momentum of the balls before the collision remains the same as the combined momentum after the collision, assuming no external forces are acting on the system.

m_A\cdot \vec{V_{A,in}}=\:\left(m_A\cdot \:\:\:\vec{V_{A,out}}\right)\cdot \left(m_B\cdot \:\:\vec{V_{B,out}}\right)

Assuming the masses of billiard balls are equal, we can obtain this equation

\:\vec{V_{A,in}}\:=\:\vec{V_{A,out}}\:\cdot \:\vec{V_{B,out}}

Based on the Pythagorean theorem, the equation mentioned indicates that the vectors VA,in, VA,out, and VB,out form a right-angled triangle. Consequently, we can represent the vector equation for the conservation of momentum with a diagram as illustrated below.

Image

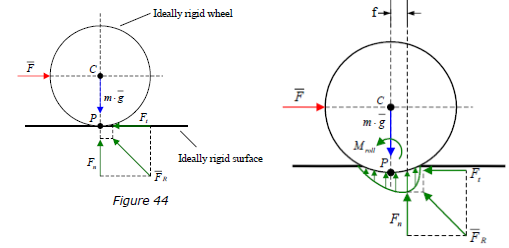
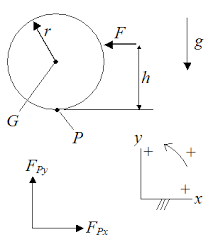
The Sweet Spot (Hitting Spot)

The sweet spot, also known as the hitting spot, on a billiard ball refers to the specific area on the surface of the ball where the cue ball or another object ball should ideally be struck for optimal results. Several factors come into play:

Transfer of Energy: Hitting the sweet spot ensures efficient transfer of energy from the cue ball to the object ball. The energy is transmitted more directly and effectively, resulting in greater control over the direction and speed of the object ball.
Transfer of Momentum: The sweet spot is typically the area where the momentum transfer is most effective during a collision. A well-executed shot at the sweet spot allows for a smoother transfer of momentum, enabling precise control over the movement and direction of both the object ball and the cue ball after the collision.
Slipping due to the friction: Rolling friction is the force that resists the motion of a rolling object, such as a ball. It is typically less than static friction, but it can still have a significant impact on the motion of an object.

Assuming ideally ball as shown on the left, where The ball touches the ground in an ideal line point (p) we can write the following system of equations:

\sum F_x\:=\:ma_x

F\:-\:F_t=\:ma_x

Since we are trying to find the height in which there is no friction we can simplify to following

F\:=\:ma_x

And also,

\sum \:F_y\:=\:ma_y

F_n\:-\:mg=\:ma_y

Since to acceleration in the Y axis

F_n\:=\:mg\:

Writing the general moment equation for rotation of a rigid body about its center of mass

\sum \:M_{roll}\:=\:I_{roll}\:\cdot \:\alpha

where,
ΣMroll represents the sum of the moments about the center of mass.

Iroll The moment of inertia of the ball about its center of mass. For solid sphere

I_{roll}\:=\:\frac{2}{5}mr^2

α The angular acceleration of the ball. Which is equal to:

\alpha \:=\:\frac{a_x}{r}

Taking into the consideration the height in which the zero friction will occur we can write the arm rule of torque moment

Image

F\left(h-r\right)\:=\:I_{roll}\cdot \frac{a_x}{r}

Substituting\:\:\: F\:=\:ma_x

solving\: for \:h\:\:\:\:ma_x\cdot \left(h-r\right)\:=\:I_{roll}\cdot \:\frac{a_x}{r}

h\:=\left(\frac{2}{5}mr^2\cdot \:\frac{1}{mr}\right)+r

Thus,

h\:=\frac{7r}{5}

This is the optimal striking height on the ball ensures no friction at point P, resulting in pure rolling motion without slipping after impact.