From Theory to Practice: A FEA Investigation of Damping

Fares Al Rwaihy

May 15, 2023

In this blog post, we will explore the concept of damping and its effect on mechanical systems. We will use Ansys FEA software to simulate the behavior of a system with and without damping and compare the results to gain a better understanding of the effects of damping

4 min read

Transient Structural Analysis Rigid Dynamics Analysis

Introduction:

Damping is an important concept in mechanical engineering as it describes the ability of a system to dissipate energy and resist motion. The damping effect can be achieved through various mechanisms, including friction, air resistance, and internal damping within the system. The presence of damping can have a significant impact on the behavior of a system, altering its natural frequency, amplitude, and stability. In order to fully understand the effects of damping, we can use FEA software to simulate the behavior of a system under different damping conditions.

Objectives:

The main objectives of this blog post are:

To establish a basic understanding of the concept of damping and its effects on mechanical systems.
To introduce Ansys FEA software as a tool for simulating the behavior of mechanical systems.

Overview

The Governing Equation

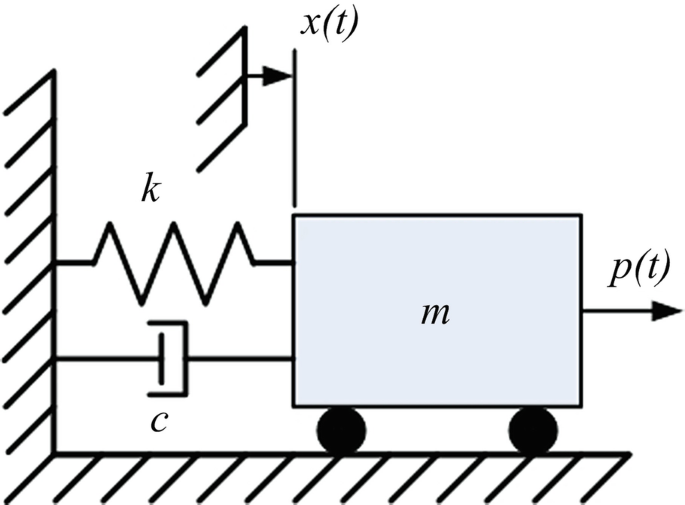
To establish the governing equation we could use the equivalent system method in which we simplify Single degree-of-freedom system (SDOF) have complex structure

Image

A mass in which dynamic external load P(t) applied, and at any instant of time we have direction of motion a(t) and forces of resistance will try to pull it back F(k): spring force, F(c) damping force. All form a system force of equilibrium

F_i+F_c+F_k\:=\:P\left(t\right)

m\cdot a+c\cdot v+s\cdot q\:=\:P_{eq}

where m is the mass of the oscillator, a is the acceleration, q is the displacement of the oscillator from its equilibrium position, t is time, c is the damping coefficient, and k is the spring constant.

so, the governing equation

m\cdot \left(q\right){''}+c\cdot \left(q\right)'+s\cdot q\:=\:P_{eq}

Free Vibration of Single Degree of Freedom Systems

Assuming that there is no external force applied then we could remove P(eq)

m\cdot \left(q\right){''}+c\cdot \left(q\right)'+s\cdot q\:=\:0

\left(q\right){''}+\frac{c}{m}\cdot \left(q\right)'+\frac{k}{m}\cdot q\:=\:0

\left(q\right){''}+2\zeta \cdot w_0\cdot \left(q\right)'+w_0^2\cdot q\:=\:0

where,

undapmed\:natural\:frequency\:w_0\:=\:\sqrt{\frac{k}{m}}

damping\:ratio\:\zeta \:=\:\frac{c}{2\cdot m\cdot w_0}

Damping coefficient

As a result of solving the previous equation by the help of 2nd order differential equations

-\zeta \cdot w_0\:\pm \sqrt{\zeta ^2-1}

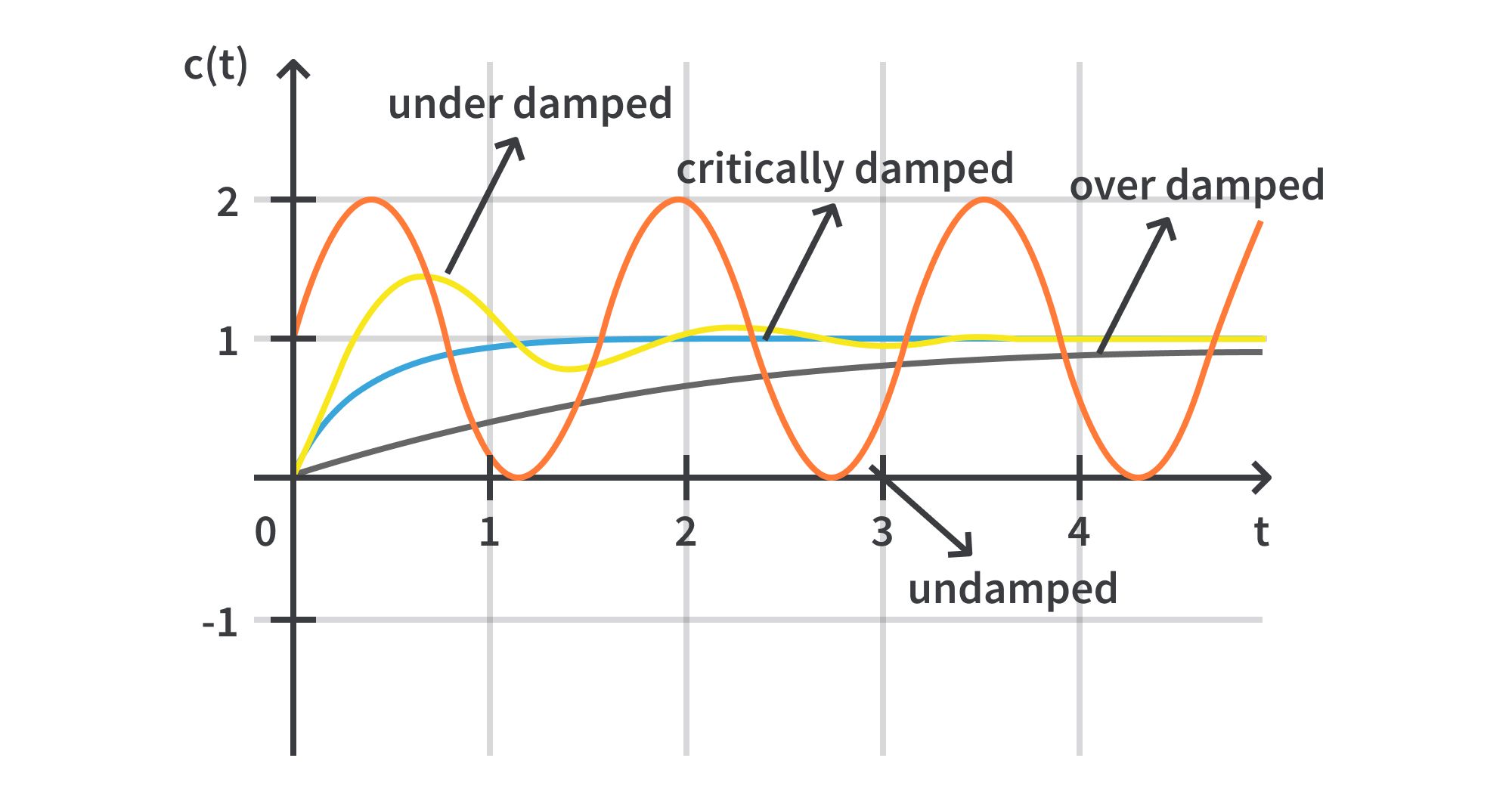
The solution to the above equation depends on the value of the damping coefficient, c, relative to the other parameters.

undamped motion: if ζ =0
under damped motion: if ζ between 0 and 1
critical damped: if ζ equal to 1
over damped: if ζ greater than 1

Image

As mentioned earlier, damping refers to the reduction in amplitude of an object's motion due to the dissipation of energy through factors such as air resistance, friction, and internal damping within the object itself. In the following, I will demonstrate the concept of damping using FEA.

Model Setup

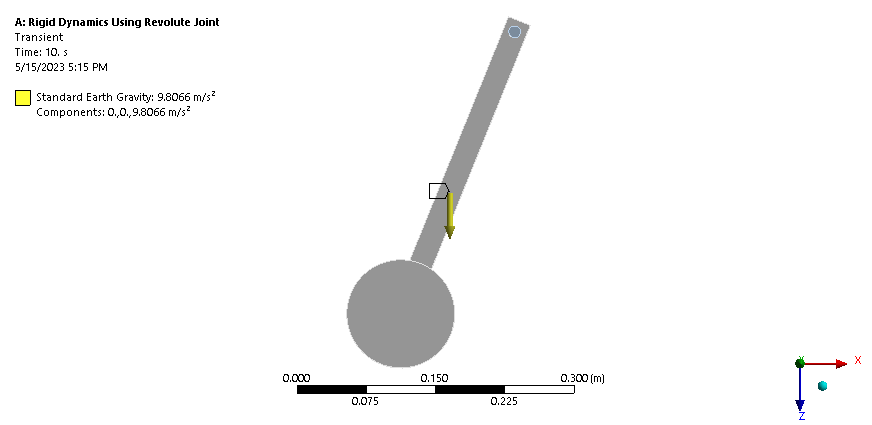
This simulation describes the workflow of simulating a pendulum moving under the gravity force and aims at showing how damping affect the dynamic movement. both Rigid body dynamics and transient structural analysis are could be used to study the influence of damping on the pendulum movement.

Rigid body dynamics: This type of analysis is used to determine the dynamic response of an assembly of rigid bodies linked by joints and springs.

Transient structural analysis: This type of analysis is used to determine the dynamic response of a structure under the action of any general time-dependent loads.

**Since we are only interested in considering the damping phenomenon and not the friction present in the pin support with the ground or between the cylindrical surface and the joint, it is better to solve it with rigid body dynamics. This approach reduces the time required for the analysis and simplifies the process.

AnsysWB results

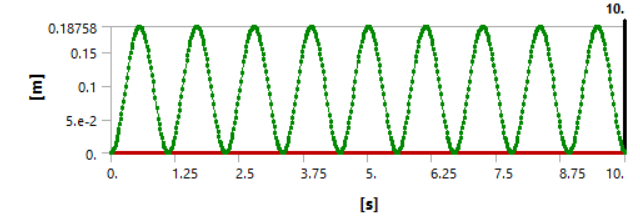
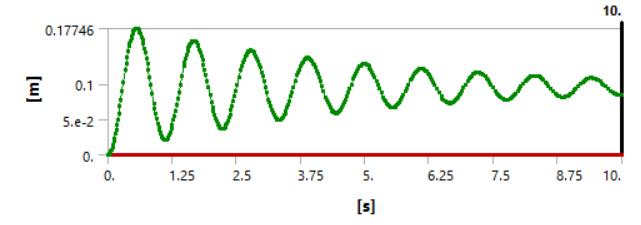
As a result of the dynamic analysis, two graphs are obtained to fully see the differences between damped and undamped pendulum

Undamped:

Damped:

Discussion

Damping is often desirable to reduce the amplitude of oscillations, making systems more stable and reliable. However, in some applications, damping can be detrimental, reducing sustain and altering sound quality. Designers must strike a balance between damping and efficient energy transfer. Mathematical models and simulation tools, such as FEA, can help optimize system design. Damping is an important field with applications in engineering, physics, and music. Understanding damping can lead to more efficient, stable, and reliable systems.