1-Dimensional Kinematics

Fares Al Rwaihy

May 15, 2023

This series of blog posts aims to compare the hand calculation and numerical simulation techniques through technical softwares

4 min read

Introduction:

The choice between hand calculation and numerical simulation using FEA is a common issue in engineering design. While hand calculations are fast and provide insight into the problem, they are limited in their ability to model complex geometries and material behaviors. On the other hand, numerical simulations using FEA can provide detailed information about stress and strain distributions, but require a significant amount of time and resources.

Objectives:

The main objective of this post is to compare hand calculations and numerical simulations through FEA in the context of 1-dimensional kinematics. The post will cover the following topics:

Overview of 1-dimensional kinematics and relevant physics laws and equations.
Hand calculation techniques for 1-dimensional kinematics problems.
Introduction to FEA and its application to 1-dimensional kinematics.

1-dimensional motion of falling object

Falling objects form an interesting class of motion problems. all fall towards the center of Earth with the same constant acceleration, regardless of their mass, as long as air resistance and friction are negligible. This acceleration is called the acceleration due to gravity, and it is constant at any given location on Earth with an average value of 9.80m/s². Although air resistance and friction can cause a lighter object to fall slower than a heavier object of the same size, for the ideal situation of free-fall, the acceleration due to gravity can be used in the kinematics equations. The direction of the acceleration due to gravity is downward, which defines what we call vertical. The value of acceleration due to gravity can be positive or negative depending on the chosen coordinate system.

Relevant physics laws and equations

1-dimensional kinematics deals with the motion of objects along a straight line. The following are the relevant physics laws and equations for 1-dimensional kinematics:

Displacement: The change in position of an object is called displacement. It is given by the equation:

\Delta x\:=\:x_f\:-\:x_i

where Δx is displacement, x_f is the final position, and x_i is the initial position.

Velocity: The rate of change of displacement is called velocity. It is given by the equation:

v\:=\:\frac{\Delta x}{\Delta t}\:

where v is velocity, Δx is displacement, and Δt is the time interval.

Acceleration: The rate of change of velocity is called acceleration. It is given by the equation:

a\:=\:\frac{\Delta v}{\Delta t}\:

where a is acceleration, Δv is the change in velocity, and Δt is the time interval.

Equations of motion: There are three equations of motion that relate displacement, velocity, acceleration, and time. These equations are

v\:=\:v_o+at

x\:=\:\:\frac{1}{2}\:\left(v_o+v\right)t

x\:=\:\:v_ot+\frac{1}{2}at^2

v^2\:=\:v_0^2+2ax

Easy way to know which equation we should use:

Equation	Variables
Equation		x	a	v	vo	t
1	-	✔	✔	✔	✔
2	✔	-	✔	✔	✔
3	✔	✔	-	✔	✔
4	✔	✔	✔	✔	-

Hand Calculation

Directional deformation using equation 3

x\:=\:\:0\cdot \left(5\right)+\frac{1}{2}\left(-9.81\right)\left(5\right)^2\:=\:122.6\:\left[m\right]

Directional velocity using equation 1, 2, or 4

v\:=\:0+\left(-9.81\right)\cdot \left(5\right)\:=\:49.05\:\left[\frac{m}{s}\right]

** 5s is the time interval considered for the free falling object

** Directional acceleration equal to the gravity acceleration -g since it is in the opposite side of z coordinate

Numerical simulation (AnsysWB)

Explicit Dynamic is the type of analysis used in ordered to capture the falling objects characteristic

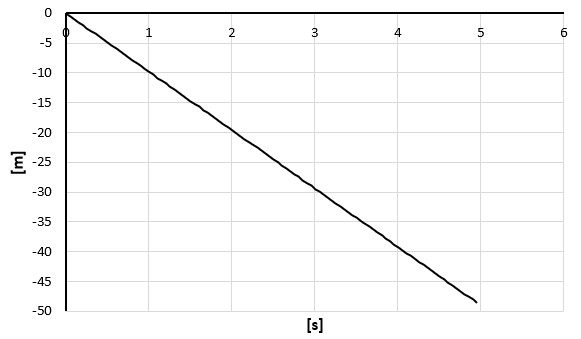
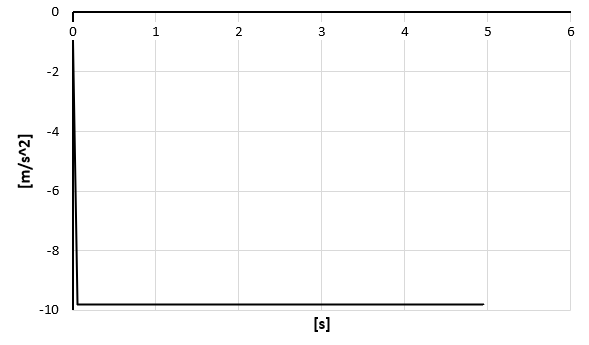
As a result of FEA analysis, 3 graphs were obtained:
Directional deformation:

Directional velocity:

Directional acceleration:

Discussion

It is impressive that the hand calculation matches the FEA simulation. However, it is important to note that there may be small differences due to the value of gravity used in the calculation and the software's time interval. In the simulation, the time interval is given to 5.006 seconds instead of the exact 5 seconds used in the hand calculation. This small difference can affect the accuracy of the results, especially if the system is sensitive to changes in time. Nevertheless, despite these differences, it is remarkable that the hand calculation and FEA simulation produce similar results, indicating the accuracy and reliability of both methods.